• Magnetwerkstoff
• Monopol

Maxwellgleichungen

Was sind die Maxwellgleichungen?

Die Maxwellgleichungen umfassen vier Prinzipe und Gesetze von elektrischen, magnetischen und optischen Erscheinungen. Sie bilden die grundlegendsten Berechnungen der Elektrodynamik. Die Maxwellgleichungen wurden vom schottischen Physiker James Clerk Maxwell zwischen 1861 und 1864 aufgestellt. Die Formeln definieren, wie elektrische und magnetische Felder zusammenhängen. Darüber hinaus wird mit den von Maxwell aufgestellten Thesen auch die Beziehung von elektrischen Ladungen und elektrischem Strom unter bestimmten Rahmenbedingungen beschrieben.

Die Maxwellgleichungen bilden heute die theoretische Grundlage für die Optik, die Elektrostatik und die Elektrotechnik. Sie sind ein komplexes System aus linearen partiellen Differenzialgleichungen der ersten Ordnung. Die Berechnungen beschreiben in ihrem Grundsatz das Verhalten von elektromagnetischen Wellen und sind daher in der Physik bis heute von großer Bedeutung.

Die vier Maxwellgleichungen und ihre Funktionen

Maxwell nahm für seine Gleichungen insgesamt vier Formeln und deren Herleitungen sowie verschiedene Ableitungen zur Hilfe, die heute nach ihm benannt sind. Der Physiker kombinierte die zu seiner Zeit bekannten Gesetzmäßigkeiten zu einer einzigen Abhandlung und ergänzte die Gleichungen um den Verschiebungsstrom. Einfach erklärt, lässt sich der physikalische Gehalt der Maxwellschen Gleichungen gut in den bekannten Gesetzen des Elektromagnetismus ausdrücken:

• Maxwellgleichung oder das Coulomb-Gesetz: Die erste Gleichung beschreibt, dass elektrische Felder D von elektrischen Ladungen (Ladungsdichte ρ) hervorgerufen werden. Die Menge der Feldlinien des elektrischen Feldes E wird durch die Divergenz eines Feldes (∇×E) charakterisieret.
  
  

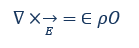
• Maxwellgleichung: Diese beschreibt, dass alle Feldlinien des magnetischen Felds B immer in sich geschlossen sind und es keine magnetischen Monopole gibt. Die Feldlinien verlaufen nicht als Vektor, sondern kreisförmig. Außerdem ist die Richtung der Feldlinien genau festgelegt: Sie beschreiben immer einen Kreis vom Nord- zum Südpol eines Magneten.
  
  

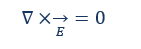
• Maxwellgleichung: Elektrische Felder und Spannungen werden durch veränderliche Magnetfelder erzeugt. Das ist die sogenannte elektromagnetische Induktion, die durch Verschiebungsströme entsteht. B steht für die magnetische Flussdichte.
  
  

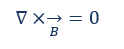
• Maxwellgleichung oder das Durchflutungsgesetz (Ampèresche Gesetze): Diese zeigt, inwiefern durch zeitlich veränderliche elektrische Felder magnetische Felder entstehen. μ0 beschreibt dabei die magnetische Permeabilität eines Vakuums beziehungsweise näherungsweise die im Luftraum. j sind die Ströme des Magnetfeldes.
  
  

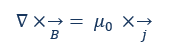
Maxwells Gleichungen beziehen sich in dieser Form stets auf die Umgebung eines luftleeren Raums. Dennoch berücksichtigt er in seinen weiteren Überlegungen die Materie anhand von materialspezifischen Parametern. Diese ist zur Beschreibung und Ausbreitung von elektrischen und magnetischen Feldern unabdingbar. Die Maxwellgleichungen haben eine Differential- sowie eine Integralform.

Warum stellten die Maxwellgleichungen das Relativitätsprinzip in Frage?

Die spezielle Relativitätstheorie (SRT) beschreibt die Bewegung von Feldern und Körpern in Raum und Zeit. Sie wurde als Erweiterung des Galileischen Relativitätsprinzip von Albert Einstein entwickelt. Die SRT legt fest, dass alle Gesetze der Physik in allen Inertialsystemen dieselbe Form haben. Das betrifft auch das Feld des Elektromagnetismus, das die Maxwellgleichungen beschreiben.

Die SRT beschreibt in ihren Grundzügen, dass Längen und Dauern individuell vom Bewegungszustand eines Betrachters abhängen. Es gibt also weder einen absoluten Raum noch eine solche Zeit. Ausgedrückt werden diese Annahmen in der mathematischen Größe Tensor. Diese basiert auf dem dreidimensionalen Raum. Auch die Maxwellgleichungen können als Spannungstensor dargestellt werden. Dieser wird als Maxwell-Tensor oder elektromagnetischer Feldstärketensor bezeichnet.

Die Gleichungen fließen in die spezielle Relativitätstheorie mit ein und beschreiben die Kräfte, die auf einen Körper in Beschleunigung wirken. Dabei sind sich Wissenschaftler lange uneins zwecks der Absolutheit von Raum und Zeit gewesen. Jahrelang konnte die Relativitätstheorie daher nicht vollständig bewiesen werden. Diese Zweifel hat Einstein dann mit dem Übergang von der Galilei- zur Lorentz-Transformation verworfen. Daher haben die Maxwellgleichungen bis heute einen festen Platz in der Relativitätstheorie.